History:
This
product has roots in one I created in 1979 (the good ole days)
and a modernization of the most unusual part in
1991. In 2020 Windows sacrificed these items during an automatic update. Given my
history, I was not about to jump ship to a normal spreadsheet. That would be a betrayal of decades of ideas, fond
memories, and a surprising level of success. So I
decided to resurrect and revamp the calculating capabilities that ignited
my fire then, but to do it better for a different purpose. T/Maker is the only spreadsheet completely
driven by arithmetic with no reliance on algebraic formulas. That is worth
preserving. Also, this is now done in Oracle's popular java language to cover Windows, Macs, and some machines with other operating systems. With some luck, perhaps I can answer a nagging
question that has haunted me since Day One. What is this thing, and what sorts of adults or adolescents would most benefit from working with it?
History:
This
product has roots in one I created in 1979 (the good ole days)
and a modernization of the most unusual part in
1991. In 2020 Windows sacrificed these items during an automatic update. Given my
history, I was not about to jump ship to a normal spreadsheet. That would be a betrayal of decades of ideas, fond
memories, and a surprising level of success. So I
decided to resurrect and revamp the calculating capabilities that ignited
my fire then, but to do it better for a different purpose. T/Maker is the only spreadsheet completely
driven by arithmetic with no reliance on algebraic formulas. That is worth
preserving. Also, this is now done in Oracle's popular java language to cover Windows, Macs, and some machines with other operating systems. With some luck, perhaps I can answer a nagging
question that has haunted me since Day One. What is this thing, and what sorts of adults or adolescents would most benefit from working with it? T/Maker: It
works with a built-in calculator. This calculator dwarfs
the power of the best of the best calculators ever held in anyone's
hand. It accepts instructions written in arithmetic across two
dimensions. It can save for you and recall any problem you ever
gave it. Depending upon your generation, the screen and syntax might
remind you of
the blackboard, green board, whiteboard, or electronic screen where
your 3rd grade
teacher displayed multiplication tables. It's where you learned that
six times
seven was and remains 42.
T/Maker: It
works with a built-in calculator. This calculator dwarfs
the power of the best of the best calculators ever held in anyone's
hand. It accepts instructions written in arithmetic across two
dimensions. It can save for you and recall any problem you ever
gave it. Depending upon your generation, the screen and syntax might
remind you of
the blackboard, green board, whiteboard, or electronic screen where
your 3rd grade
teacher displayed multiplication tables. It's where you learned that
six times
seven was and remains 42. Calculation Trails:
 The unit of work in T/Maker is not a formula like all other spreadsheets but something called a calculation trail.
The unit of work in T/Maker is not a formula like all other spreadsheets but something called a calculation trail.
Travel around the screen while pushing calculator buttons to store/fetch data and calculate with it.
Each trail is put on a separate screen. Trails can be restarted numerous times from different locations.
A trail is composed of steps. Steps have numbers to establish the order of calculation.
Each step is located over a cell. That mIght facilitate interactions with the cell or maybe clarify the purpose.
A trail, unlike a formula, can calculate and place many values anywhere in the grid from anywhere else.
With a bit of experience, trails can be read left to right with the same ease (but greater thrills) than Dick and Jane books.
You won't be needing the skin of your teeth, the seat of your pants, or a wing and a prayer for basic math manipulations.
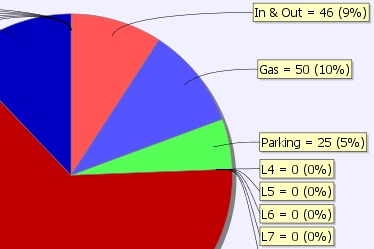
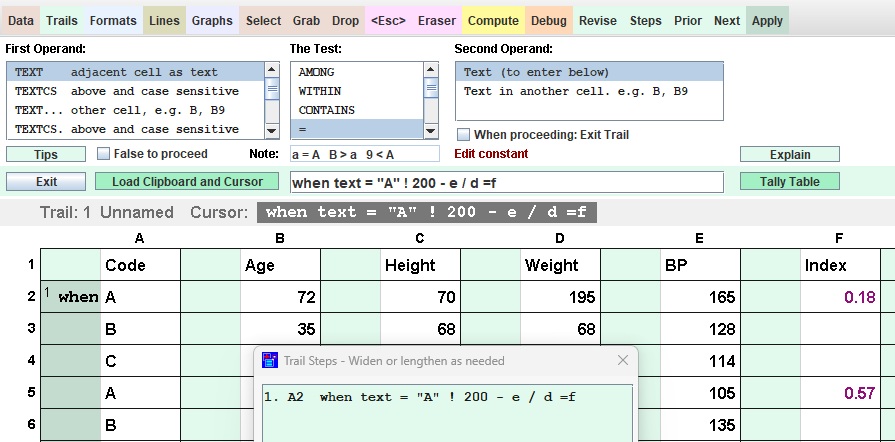
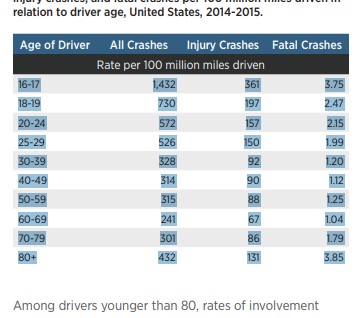
Newsworthy Example: Here is a calculation in the news recently. Columns A through F were obtained from the NY Times.
Column G is calculated by T/Maker using the known formula but without rounding to whole numbers.
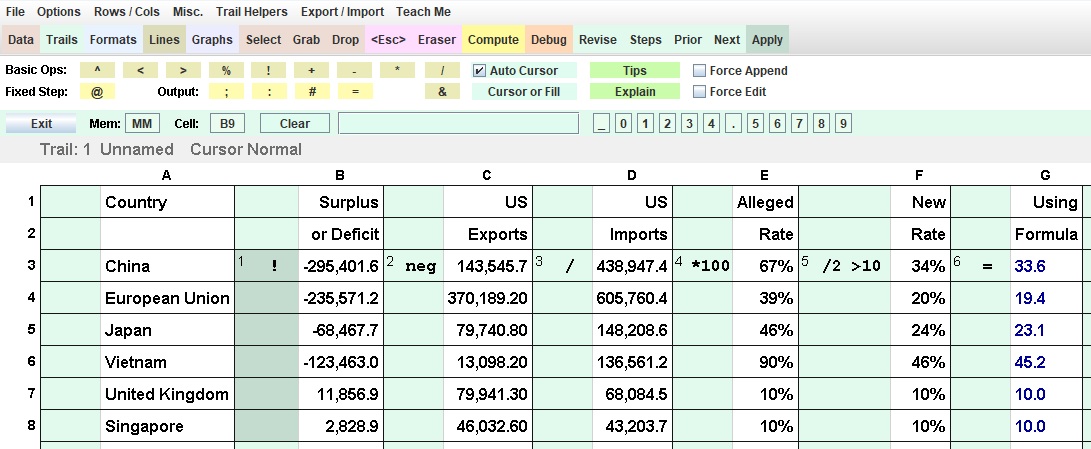
| Trails Screen: The Math Lite Toolbar is shown. 2 cells for each column. Green for math. White for text and data. This solution has been chosen to do the calculation and be illustrative. Let's introduce some abbreviations: Cal will be the value in T/Maker's calculator Adj will be the adjacent value (in the white cell) for the step in question. iTc will stand for "in This case" Step 1. An exclamaiton point operator sets Cal to iTc Adj Step 2. neg is a function that changes the sign of Cal, iTc negative to positive Step 3. Cal is divided by iTc Adj Step 4. Cal is multiplied by 100. Step 5. Cal is divided by 2 and set to the maximum of itself and 10 Step 6. The equal sign sets iTc Adj equal to Cal and clears Cal to zero This trail is excuted starting at all darkened green cells beginning with row 3. These cells were darkend by clicking on the Apply Button and then the cells. Syntactical Glitch: Do not enter a negative number as an operand. T/Maker interprets - (dash) as subtraction operator. Use _ (the underscore character) instead. Wrong: *-3 (intended to multiply by -3). Right: *_3 |
When operators can be followed by an operand but are not, the corresponding operand is assumed to be the Adj. This is the case for steps 1, 3, and 6. Step 2 is a function that operates on Cal and needs no operand. Steps 4 and 5 (both of 5's operations) specify constants for the operand. An operand used in a step can be specified by the letter of its column (case insensitive). The row is assumed to be the same as the one the step is located on. The above 6-step process could have been written as just one step and put in any column. That step is shown below. b, d, and g are the column names used in this example. This technique often saves time and adds clarity. Four constants are used. neg is a function. There are 5 operators total. All have an operand specified. Thus, no Adj is used as such. !b neg /d *100 /2 >10 =g It is amazing what the consequences of these 18 characters have been. |




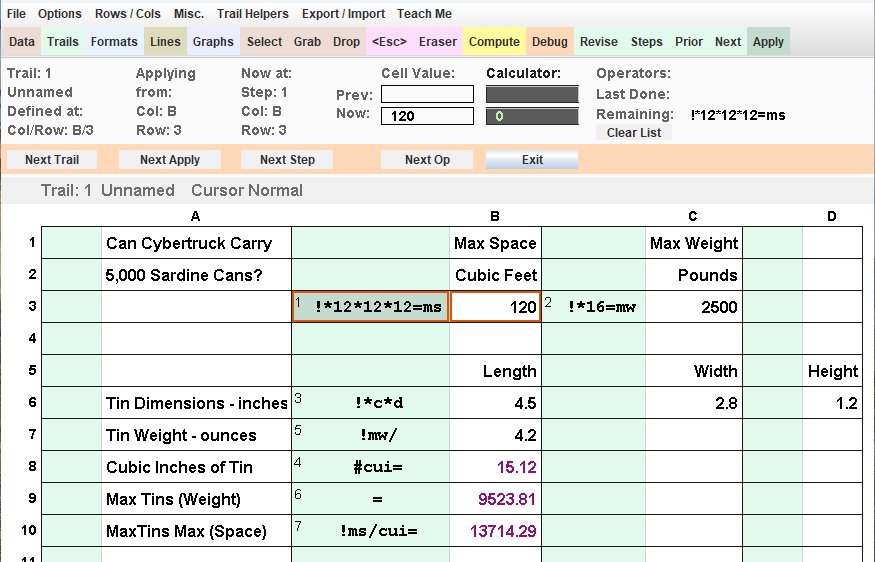
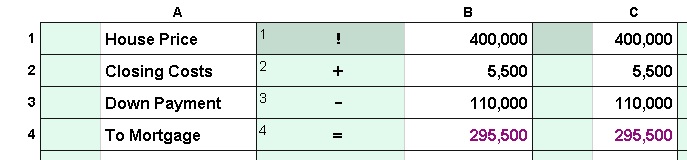
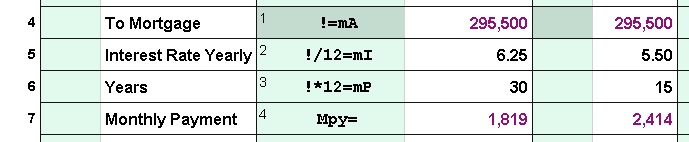

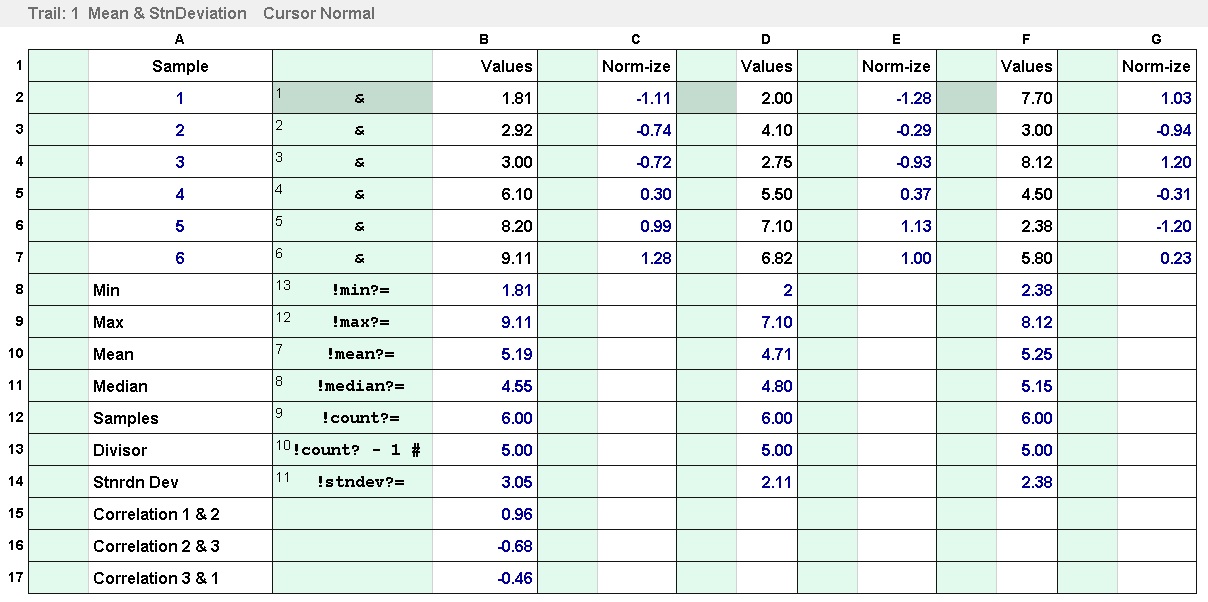
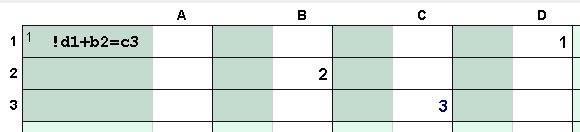







 Memory names must start with 2 letters which can be followed by letters or numbers.
Memory names must start with 2 letters which can be followed by letters or numbers. Cell names use a single letter for the column followed by the
row number. Case insensitive.
Cell names use a single letter for the column followed by the
row number. Case insensitive.




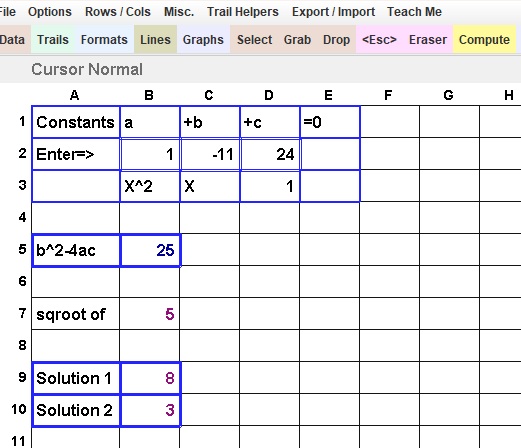
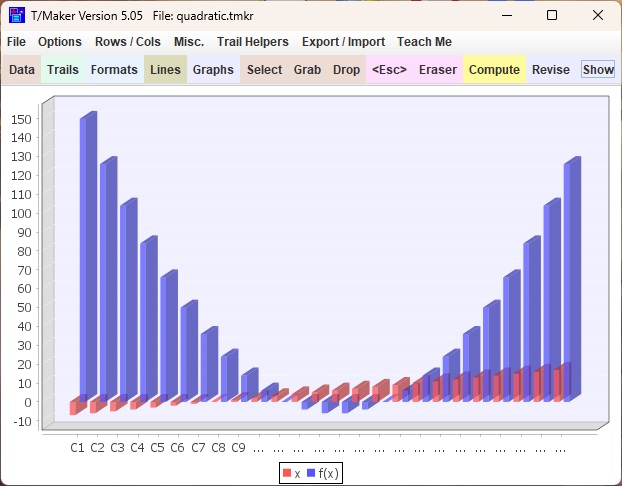
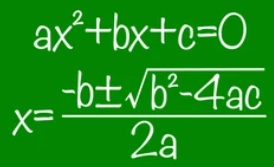 The Quadratic:
The Quadratic: